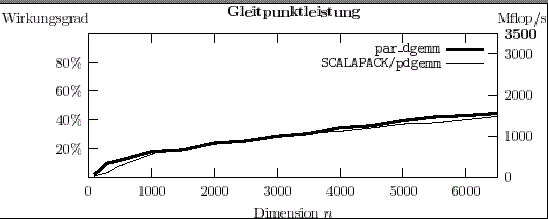
Abbildung 1: Matrizenmultiplikation auf 10 Prozessoren des Wiener PC-Clusters (Maximalleistung: 3.5 Gflop/s). Das HPF-Programm par_dgemm erreicht eine ähnliche Gleitpunkt- leistung wie das SCALAPACK-Programm pdgemm.
In den letzten Jahren hat die Idee, handelsübliche PCs oder Workstations
mit gängiger Netzwerktechnik so zu verbinden, dass sie dem Benutzer wie
ein einzelner Parallelrechner erscheinen, einen enormen Aufschwung erlebt.
Die Gründe dafür sind die starke Leistungszunahme der Prozessoren und Netzwerkkomponenten
und deren drastischer Preisverfall. Mittlerweile befinden sich mehrere
PC-Cluster in der Liste der weltweit schnellsten Computer.1
Beowulf-Cluster2, wie (bestimmte) PC-Cluster auch genannt werden, sind aus
handelsüblichen PCs aufgebaut, die durch ein Kommunikationsnetzwerk verbunden
sind und gemeinsam (parallel) an der Lösung eines Problems arbeiten. Dabei
handelt es sich meist um Computer mit Intel- oder verwandten Prozessoren
(wie z. B. den Athlon-Prozessoren von AMD), aber auch Alpha-Prozessoren
werden in solchen Computer-Systemen verwendet. Meistens gibt es einen Server-PC
und mehrere Client-PCs, die die eigentlichen Berechnungen durchführen.
Der Server-PC dient als Systemkonsole und Fileserver. Er stellt auch die
Verbindung zum Internet her. Bei großen Clustern können auch mehrere Server-PCs
vorhanden sein, die verschiedene Aufgaben übernehmen. Die Client-PCs haben
keine direkte Verbindung zur "Außenwelt", meistens auch keine Tastaturen
und Bildschirme, und werden nur über "remote login" angesprochen.
Eine typische Konfiguration wäre etwa eine Verbindung von 8 - 32 PCs (mit je einem, zwei oder vier Prozessoren) über Fast-Ethernet oder schnellere Netzwerke wie Gigabit-Ethernet3, Myrinet4 oder SCI5 (Scalable Coherent Interface). Aber auch größere Cluster mit über 100 Prozessoren haben sich bereits als erfolgreich erwiesen.
Als Parallelrechner sind PC-Cluster zwischen MPPs (Massively Parallel Processors) und NOWs (Networks of Workstations) positioniert. PC-Cluster profitieren dabei von den Entwicklungen in beiden Architekturklassen. MPPs haben üblicherweise eine größere Anzahl von Prozessoren und schnellere Kommunikationseinrichtungen. Typische Probleme bei der Programmierung von MPPs sind die gleichmäßige Last- und Datenverteilung, die Wahl der geeigneten Parallelitätsebene der Algorithmen (Programmanweisungen, Datenparallelität, parallele Prozesse) und die Minimierung des Kommunikations-Overheads. Programme, die keine allzu feinkörnige Struktur erfordern, können meist problemlos auf PC-Cluster portiert werden und laufen dort sehr effizient. Die Programmierung von NOWs dient meist dem Versuch, unbenutzte Rechenzeit auf leistungsfähigen Workstations zu nutzen. Das erfordert Algorithmen, die extrem tolerant auf Leistungsschwankungen der beteiligten Workstations reagieren und daher eine sehr effiziente dynamische Lastverteilung besitzen müssen. Programme, die auf NOWs zufrieden stellend laufen, sind meist ebenso gut auf PC-Clustern lauffähig.
Als Betriebssystem wird vornehmlich Linux verwendet, das für viele Anwendungen aus dem technisch-naturwissenschaftlichen Bereich die ideale Grundlage darstellt: es ist (nahezu) kostenlos verfügbar, hat eine ausgezeichnete Stabilität und ermöglicht den Einsatz von jahrelang entwickelter und erprobter Software auch auf billigen Standard-PCs. Ein spezieller Vorteil von Linux gegenüber anderen Unix-Varianten für Standard-PCs ist die gute und schnelle Verfügbarkeit von Treibern für fast alle Hardwarekomponenten.
Mit vielen Anwendungsprogrammen können auf Standard-PCs bereits empirische Leistungswerte erzielt werden, die mit jenen von Workstations konkurrieren können. Dies ist u. a. darauf zurückzuführen, dass technische Neuerungen wegen der kürzeren Produktlebenszyklen der PCs schneller in die aktuellen Modelle aufgenommen werden. Allerdings führt dies zu einer erheblich rascheren Veralterung der PC-Hardware.
|
Tätigkeit
|
Aufwand in Stunden
|
|
Hardwareplanung
|
80
|
|
Hardwarebeschaffung
|
20
|
|
Erstinstallation
|
120
|
|
Betrieb 2 Jahre
|
110
|
|
Summe
|
330
|
Tabelle 1: Richtwerte für den Personalaufwand bei Errichtung und Betrieb eines PC-Clusters.
Eine Übersicht über den für die Errichtung und den Betrieb dieses PC-Clusters erforderlichen Personalaufwand enthält Tabelle 1. Die Werte in dieser Tabelle gelten für Personen mit Erfahrung im (parallelen) Hochleistungsrechnen und beim Installieren und Betrieb von Linux-Systemen. Falls dieses Vorwissen nicht vorhanden ist, muss ein entsprechend größerer Aufwand einkalkuliert werden. Die Gesamtbetriebsdauer des Clusters wurde mit zwei Jahren angenommen. Zum Vergleich: vor drei Jahren waren bei PCs gerade Intel Pentium 200 MMX Prozessoren hochaktuell, die heute niemand mehr im Hochleistungsrechnen einsetzen würde, auch wenn sie noch problemlos funktionieren.
Die Programmierung des PC-Clusters kann auf verschiedene Arten erfolgen:
Zu Testzwecken wurde uns freundlicherweise von der RWTH Aachen deren Siemens-PC-Cluster12 zur Verfügung gestellt. Dieser betriebsfertig ausgelieferte hpcLine-Cluster besteht aus 16 Doppelprozessor-PCs mit 400 MHz Pentium II-Prozessoren, 512 KB Level 2 Cache, 512 MB Hauptspeicher und lokalen 4 GB Festplatten. Die PCs kommunizieren entweder über ein Fast-Ethernet- oder ein SCI-Netzwerk, das als zweidimensionaler Torus konfiguriert ist.
Das Betriebssystem ist auch auf diesem Cluster Linux (Red Hat, Kernel 2.0.36 im SMP Modus).
Die SGI Origin2000 ist modular aufgebaut. Jeweils zwei MIPS R10000-Prozessoren (mit 250 MHz Taktfrequenz) befinden sich auf einem Node-board. Die einzelnen Node-boards sind über Router-boards miteinander verbunden (Hypercube-Topologie, 780 MByte/s Bandbreite). Der Hauptspeicher ist auf die einzelnen Node-boards verteilt. Jeder Prozessor kann auf den gesamten Hauptspeicher zugreifen, die Zugriffszeiten auf einzelne Speicheradressen sind aber nicht einheitlich (cache coherent non uniform memory access, ccNUMA-Architektur).
Für die Parallelprogrammierung stehen folgende Möglichkeiten zur Verfügung:
Auch bei Algorithmen mit größerem Kommunikationsbedarf, z. B. Algorithmen aus der Linearen Algebra, kann mit speziellen Maßnahmen (z. B. mit den verschiedenen Formen des Blockens; Ueberhuber [9]) akzeptable Gleitpunktleistung trotz langsamer Netzwerke erzielt werden. Allerdings muss bei langsamen Netzwerken die Kommunikationsstrategie sehr sorgfältig gewählt werden.
Numerische Experimente wurden mit verschiedenen Implementierungen dieser zwei Algorithmen durchgeführt. Als Vergleichsbasis dienten dabei die entsprechenden Programme aus SCALAPACK, einem Programmpaket auf MPI- und PVM-Basis, das im Parallelrechnen eine ähnlich wichtige Rolle spielt wie LAPACK auf sequentiellen Computern.
Neben den SCALAPACK-Programmen wurden u.a. selbstentwickelte HPF-Programme getestet. Dabei konnte der Nachweis geführt werden, dass es mit HPF-Programmen möglich ist, die Leistungswerte von MPI-Programmen zu erreichen oder sogar zu übertreffen (siehe Abb. 1).

Abbildung 1: Matrizenmultiplikation auf 10 Prozessoren des Wiener PC-Clusters (Maximalleistung: 3.5 Gflop/s). Das HPF-Programm par_dgemm erreicht eine ähnliche Gleitpunkt- leistung wie das SCALAPACK-Programm pdgemm.
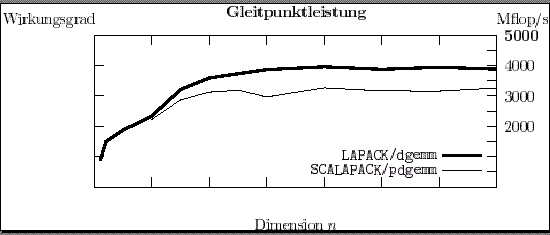
Abbildung 2: Matrizenmultiplikation auf 10 Prozessoren einer SGI Origin (Maximalleistung: 5 Gflop/s). Das speziell für die SGI Origin 2000 parallelisierte LAPACK-Programm dgemm liefert etwas bessere Gleitpunktleistung als das SCALAPACK-Programm pdgemm.
Die Experimente mit den Programmen zur Cholesky-Faktorisierung zeigen sehr deutlich, wie sich die Kommunikationsgeschwindigkeit in einem PC-Cluster auf die Gleitpunktleistung auswirken kann. Mit Fast-Ethernet-Kommunikationsnetzwerk sind nur enttäuschende Leis-tungswerte erreichbar (siehe Abb. 3). Mit dem schnelleren SCI-Netzwerk kann zufrieden stellende Gleitpunktleistung erzielt werden (siehe Abb. 4).
Diese Resultate sind charakteristisch für den kommunikationsintensiven Parallelismus von Algorithmen der Linearen Algebra. Die Abbildungen 3 und 4 zeigen auch deutlich ein (besonders auf PC-Clustern auftretendes) Leistungsverhalten: Für jede Problemgröße gibt es eine kritische Anzahl von Prozessoren, ab der keine weiteren Leistungssteigerungen mehr erzielt werden können. Die sinnvolle Maximalgröße eines PC-Clusters richtet sich nach den geplanten Anwendungen.
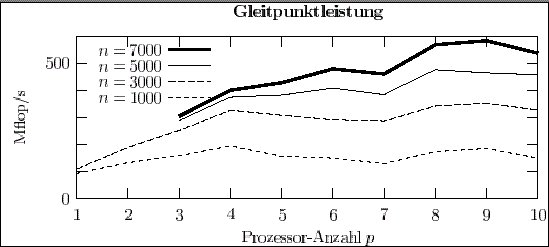
Abbildung 3: Cholesky-Faktorisierung symmetrischer, positiv definiter Matrizen der Dimension n = 1000, ..., 7000 auf p = 1,2, ...,10 Prozessoren des Wiener PC-Clusters (Kommunikation durch Fast Ethernet, Maximalleistung: p 350 Mflop/s) mit Hilfe des SCALAPACK-Programms pdpotrf.
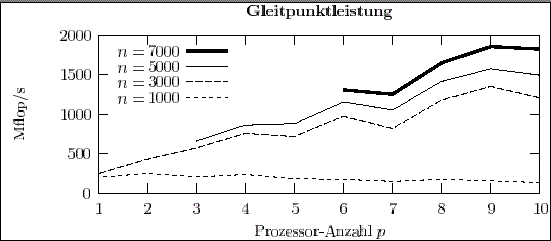
Abbildung 4: Cholesky-Faktorisierung symmetrischer, positiv definiter Matrizen der Dimension n = 1000, ..., 7000 auf p = 1,2, ...,10 Prozessoren des Aachener PC-Clusters (Kommunikation durch SCI, Maximalleistung: p 400 Mflop/s) mit Hilfe des SCALAPACK-Programms pdpotrf.
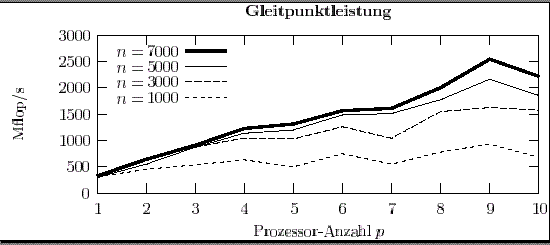
Abbildung 5: Cholesky-Faktorisierung symmetrischer, positiv definiter Matrizen der Dimension n = 1000, ..., 7000 auf p = 1,2, ...,10 Prozessoren der SGI Origin2000 des ZID der TU Wien (Maximalleistung: p 500 Mflop/s) mit Hilfe des SCALAPACK-Programms pdpotrf.
In vielen großen Anwendungsprogrammen ist ein kommunikationsarmer Task-Parallelismus anzutreffen. Um auch auf diesem Gebiet Erfahrungen zu sammeln, wurde das Programmpaket WIEN 97 herangezogen.
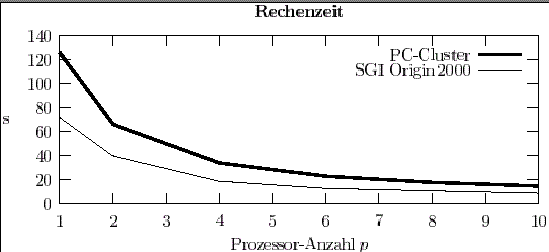
Abbildung 6: Ein Programmlauf von WIEN 97 auf p = 1,2, ...,10 Prozessoren. Um die gleiche Laufzeit zu erzielen, benötigt man am Wiener PC-Cluster doppelt so viele Prozessoren wie auf der SGI Origin 2000.
Mit einer parallelen Version des Programmpaketes WIEN 97 wurden auf dem Wiener PC-Cluster und auf der SGI Origin 2000 des ZID der TU Wien Laufzeituntersuchungen angestellt. Die gewählte Parallelisierung beruht auf der Verteilung von größeren Tasks über Shell-Scripts. Die Prozessoren rechnen jeweils mehrere Minuten unabhängig voneinander, die Kommunikation findet über Dateien statt. Die Effizienz dieser Parallelisierungsmethode ist üblicherweise sehr hoch (siehe Abb. 6 und Tabelle 2), sie wird nur durch Lastverteilungseffekte - es gibt nur eine begrenzte Anzahl an Tasks - und kurze sequentielle Programmteile begrenzt.
|
PC-Cluster
|
SGI Origin 2000
|
|||
|
p
|
Laufzeit
|
Speed-up
|
Laufzeit
|
Speed-up
|
|
1
|
126.3
|
1
|
72.0
|
1
|
|
2
|
66.5
|
1.9
|
40.5
|
1.8
|
|
4
|
34.1
|
3.7
|
19.3
|
3.7
|
|
6
|
23.4
|
5.4
|
13.5
|
5.3
|
|
8
|
18.3
|
6.9
|
11.9
|
6.1
|
|
10
|
15.9
|
7.9
|
9.8
|
7.3
|
Tabelle 2: Laufzeit und Speed-up für die Berechnung der Elektronendichte des Hochtemperatursupraleiters YBaCuO7 mittels WIEN 97 auf 1-10 Prozessoren des Wiener PC-Clusters und der SGI Origin 2000 des ZID.

Abbildung 7: Simulation der Cholesky-Faktorisierung mit CLUE (n = 2000).
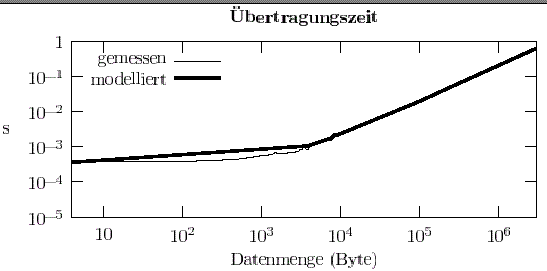
Abbildung 8: Performance der Kommunikation zwischen zwei Knoten eines PC-Clusters mit Fast Ethernet Netzwerk.
Eine Unterstützung bei der Entscheidung für eine bestimmte Konfiguration kann durch Simulation gegeben werden. Für diesen Zweck wurde das Simulationssystem CLUE (CLUSTER EVALUATOR, Hlavacs et al.[4]) entwickelt. Dabei steht die Simulation von PVM-basierten Programmen im Mittelpunkt, es können aber auch MPI-basierte Programme erfolgreich simuliert werden.
Die simulierten Anwendungsprogramme laufen in praktisch unveränderter Form, nur eine Neuübersetzung und das Linken mit der Simulationsbibliothek MISS-PVM (siehe Kvasnicka, Ueberhuber [5]) ist notwendig. Die Simulationsgeschwindigkeit ist abhängig vom Computer, auf dem die Simulation durchgeführt wird. Da alle (parallelen) Teile wirklich ausgeführt werden, dauert der Simulationslauf mindestens so lange wie die Summe der Laufzeiten der parallelen Teile. Dazu kommt noch die Simulation der Kommunikation, die bei den meisten gut parallelisierbaren Algorithmen aber sehr rasch abläuft. Wenn notwendig (und im geplanten Netzwerk wirklich vorhanden) können auch Überlastsituationen (contention) simuliert werden.
Tabelle 3 gibt einen Kostenvergleich zwischen dem PC-Cluster und dem Hochleistungsserver der TU Wien. Beim PC-Cluster wurde ein Stundensatz von ATS 280 für vorhandenes (Hochschul-)Personal angenommen (inklusive Lohnnebenkosten). Für externes Personal wurde nach den Honorarrichtlinien für EDV-Dienstleistungen der Wirtschaftskammer ein Stundensatz von ATS 1400 (inkl. 20 % MWSt.) zugrunde gelegt. Die Kosten für die SGI Origin 2000 entsprechen der Kostenstellenrechnung des ZID der TU Wien und inkludieren Hardware/Software-Kosten sowie anteiligen Personalaufwand.
|
Hardware und System-
|
Personal
|
Gesamtkosten
|
|
|
PC-Cluster -
|
240 000,-
|
90 000,-
|
330 000,-
|
|
PC-Cluster -
|
240 000,-
|
460 000,-
|
700 000,-
|
|
SGI Origin 2000, p Proz.
|
p x 145 000,-
|
Tabelle 3: Gesamtkosten (in ATS) für 2 Jahre für einen PC-Cluster mit 10 Prozessoren, der entweder durch eigenes oder durch externes Personal errichtet und gewartet wird, sowie für die SGI Origin 2000.
Zusätzliche Kosten für ein schnelleres Netzwerk am PC-Cluster belaufen sich derzeit auf etwa ATS 20 000 pro Rechenknoten für die Hardware. Auch mit entsprechend höherem Installationsaufwand ist zu rechnen. Damit kann auch für kommunikationsintensive Algorithmen eine vernünftige Gleitpunktleistung erreicht werden (siehe Abb. 4), die Kosten steigen aber proportional zum Leistungsgewinn.
|
Nutzungsdauer
|
|
||||
|
1
|
5
|
10
|
20
|
30
|
|
|
1
|
6 000
|
30 000
|
60 000
|
120 000
|
180 000
|
|
6
|
35 000
|
175 000
|
350 000
|
700 000
|
|
|
18
|
105 000
|
525 000
|
|||
Tabelle 4: Gesamtkosten (in ATS) für 2 Jahre Nutzung von p Prozessoren der SGI Origin 2000 bei einer täglichen (durchschnittlichen) Nutzungsdauer von 1, 6 oder 18 Stunden.
Wenn man die Gesamtkosten aus Tabelle 3 vergleicht, dann ergibt sich, dass mit den Kosten des PC-Clusters ungefähr drei bis sechs Prozessoren des Hochleistungsservers zwei Jahre lang durchgehend finanziert werden können.
Abgesehen davon, dass für den universitären Anwender (derzeit noch) keine direkten Kosten für die Verwendung des Hochleistungsservers anfallen, ist diese Dar-stellung auch noch aus einem anderen Grund unrealistisch: Der Betreiber eines PC-Clusters trägt tatsächlich die vollen Kosten, unabhängig davon, wie lange der Cluster unbenutzt leer steht. Die Verwendung eines Zentralservers, der einer Vielzahl verschiedener Benutzer zur Verfügung steht, verursacht aber - vom Standpunkt des Anwenders - nur Kosten, wenn er tatsächlich verwendet wird. Damit verringern sich aber die Kosten des Zentralservers dramatisch (siehe Tabelle 4) und der PC-Cluster kommt aus Kostenüberlegungen kaum mehr in Betracht.
Beim Kostenvergleich muss noch ein wesentlicher Unterschied zwischen einem PC-Cluster und einem zentralen Hochleistungsserver berücksichtigt werden: Der PC-Cluster steht seinem Besitzer jederzeit vollständig zur Verfügung (auch wenn er ihn unbenützt leer stehen lässt). Zentrale Server werden von vielen Benutzern im Multi-user-Betrieb gleichzeitig verwendet. Die Gesamtauslas-tung eines Servers ist damit höher und gleichmäßiger. Die Antwortzeit kann allerdings länger ausfallen als die z. B. in Abb. 5 dargestellte Laufzeit.
Ein schwer zu quantifizierender Kostenfaktor sind die Unsicherheiten, die es bei Errichtung und Betrieb eines PC-Clusters gibt. Es kann z. B. zu Schwierigkeiten kommen, wenn Software- und Hardware-Komponenten, die aus unterschiedlichen Quellen stammen, nicht reibungslos miteinander funktionieren oder Leistungsengpässe bewirken. Bei Anschaffung eines fertig konfigurierten PC-Clusters (wie jenem der RWTH Aachen) ist es Sache des Anbieters, mit diesen Schwierigkeiten fertig zu werden. Allerdings kostet ein solches Computer-System deutlich mehr als ein selbsterrichteter PC-Cluster.
PC-Cluster stellen für bestimmte Anwendungen eine alternative zu den großen Zentralrechnern dar. Seriöse Kostenvergleiche gehen allerdings deutlich zu Gunsten der zentralen Hochleistungsserver aus.
[2] R. Buyya (Ed.), High Performance Cluster Computing: Architecture and Systems, Prentice Hall, Upper Saddle River, 1998.
[3] R. Buyya (Ed.), High Performance Cluster Computing: Programming and Applications, Prentice Hall, Upper Saddle River, 1998.
[4] H. Hlavacs, D. F. Kvasnicka, C. W. Ueberhuber, CLUE- Cluster Evaluation, Technical Report AURORA TR 2000-05, Vienna University of Technology, 2000, www.vcpc.univie.ac.at/aurora/publications/.
[5] D. F. Kvasnicka, C. W. Ueberhuber, Developing Architecture Adaptive Algorithms using Simulation with MISS-PVM for Performance Prediction, Proceedings of the International Conference on Supercomputing, ACM, 1997, pp. 333-339.
[6] G. F. Pfister, In Search of Clusters, 2nd ed., Prentice Hall, Upper Saddle River, 1998.
[7] D. J. Singh, Planewaves, Pseudopotentials and the LAPW Method, Kluwer, Dordrecht, 1994.
[8] T. L. Sterling, J. Salmon, D. J. Becker, D. F. Savarrese, How to Build a Beowulf, MIT Press, 1999.
[9] C. W. Ueberhuber, Numerical Computation, Springer-Verlag, Heidelberg, 1997.
[10] B. Wilkinson, M. Allen, Parallel Programming Techniques and Applications Using Networked Workstations and Parallel Computers, Prentice Hall, Upper Saddle River, 1999.